命題20
相似な多角形は同数で相似な三角形、しかも全体と同じ比の三角形に分割される。そして、多角形は対応している辺が対応している辺に対する比の2乗比を持つ。
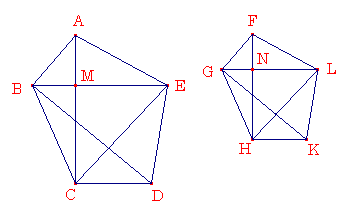
ABCDEとFGHKLを相似な多角形とし、ABをFGに対応するとする。
多角形ABCDEとFGHKLが相似な三角形で、三角形は量において等しく、全体と同じ比に分けられ、多角形ABCDEは多角形FGHKLにABがFGに持つ比の2乗の比を持つことをいう。
BE、CE、GL、HLを結ぶ。
さて、多角形ABCDEが多角形FGHKLと相似であるから、それゆえに∠BAEは∠GFLと等しく、そしてABはAEに対し同じようにGFはFLに対する。definitionⅥ.1
それからABEとFGLが1つの角が1つの角と等しく、そして等しい角のまわりの辺が比例している2つの三角形であるから、それゆえに⊿ABEは⊿FGLと対応する角が等しく、つまりそれはまた相似であり、それゆえに∠ABEは∠FGLと等しい。propositionⅥ.6、propositionⅥ.4、definitionⅥ.1
しかし多角形の相似のために全体の∠ABCは全体の∠FGHと等しく、それゆえに余りの∠EBCは余りの∠LGHと等しい。
そして、⊿ABEと⊿FGLは相似であるから、BEはABに対し同じようにGLはGFに対する。また、多角形は相似であるから、ABはBCに対し同じようにFGはGHに対する。それゆえに、等間隔比で、BEはBCに対し同じようにGLはGHに対し、つまり、等しい∠EBCと∠LGHのまわりの辺は比例している。それゆえに⊿EBCは⊿LGHと対応する角が等しい、つまり⊿EBCはまた⊿LGHと相似である。propositionⅤ.22、propositionⅥ.6、propositionⅥ.4、definitionⅥ.1
同じ理由で⊿ECDはまた⊿LHKと相似である。
それゆえに相似な多角形ABCDEとFGHKLは量の等しい、相似な三角形に分けられる。
それらはまた全体と同じ比である、つまりABE、EBC、ECDは前項であり、FGL、LGH、LHKが後項であるとき、三角形は比例している、そして多角形ABCDEが多角形FGHKLに対応している辺が対応している辺に持つ、つまりABがFGに持つ比の2乗の比を持つことをいう。
ACとFHを結ぶ。
それから多角形は相似であるから、∠ABCは∠FGHと等しく、そしてABはBCに対し同じようにFGはGHに対し、⊿ABCは⊿FGHと対応する角が等しく、それゆえに∠BACは∠GFHと等しく、そして∠BCAは∠GHFと等しい。propositionⅥ.6
そして、∠BAMは∠GFNと等しく、そして∠ABMもまた∠FGNと等しいから、それゆえに余りの∠AMBもまた余りの∠FNGと等しい。それゆえに⊿ABMは⊿FGNと対応する角が等しい。propositionⅠ.32
同じように⊿BMCはまた⊿GNHと対応する角が等しいことが証明できる。
それゆえに、比例して、AMはMBに対し同じようにFNがNGに対し、そしてBMがMCに対し同じようにGNがNHに対する。だから、その上、等間隔比で、AMはMCに対し同じようにFNはNHに対する。propositionⅤ.22
しかし、三角形はそれらの辺と同じように互いに対するから、AMはMCに対し同じように⊿ABMは⊿MBCに対し、そして同じように⊿AMEは⊿EMCに対する。propositionⅥ.1
それゆえにまた前項の1つは後項の1つに対し同じように前項のすべては後項のすべてに対し、それゆえに⊿AMBは⊿BMCに対し同じように⊿ABEは⊿CBEに対する。propositionⅤ.12
しかし⊿AMBは⊿BMCに対し同じようにAMはMCに対し、それゆえにAMはMCに対し同じように⊿ABEは⊿EBCに対する。propositionⅤ.11
同じ理由でまたFNはNHに対し同じように⊿FGLは⊿GLHに対する。
そしてAMはMCに対し同じようにFNはNHに対し、それゆえに⊿ABEは⊿BECに対し同じように⊿FGLは⊿GLHに対し、そして、入れ替えて、⊿ABEは⊿FGLに対し同じように⊿BECは⊿GLHに対する。propositionⅤ.11、propositionⅤ.16
同じように、BDとGKが結ばれるならば、⊿BECが⊿LGHに対し同じように⊿ECDが⊿LHKに対することを証明できる。
そして⊿ABEが⊿FGLに対し同じように⊿EBCが⊿LGHに対し、そしてさらに同じように⊿ECDが⊿LHKに対するから、それゆえにまた前項の1つは後項の1つに対し同じように前項の和は後項の和に対する。それゆえに⊿ABEは⊿FGLに対し同じように多角形ABCDEは多角形FGHKLに対する。propositionⅤ.12
しかし、相似な三角形が対応する辺の2乗比であるために、⊿ABEは⊿FGLに対応する辺ABが対応する辺FGに持つ比の2乗の比を持つ。propositionⅥ.19
それゆえに多角形ABCDEもまた多角形FGHKLに対応する辺ABが対応する辺FGに持つ比の2乗比を持つ。propositionⅤ.11
それゆえに、相似な多角形は同数で相似な三角形、しかも全体と同じ比の三角形に分割される。そして、多角形は対応している辺が対応している辺に対する比の2乗比を持つ。
証明終了
系
同じようにまたそれらが対応する辺の2乗比であることを四辺形の場合で証明できる。そしてそれはまた三角形の場合で証明されて、それゆえにまた、一般に、相似な直線図形は対応する辺の2乗比で互いに対する。